A Theory of Sequences in cvc5

Introduction

The theory of sequences in cvc5 is relatively new. In essence, it is meant to model data structures such as List in Java, or std::vector in c++. Unlike the theory of arrays (which is actually a theory of maps), the theory of sequences is very rich, and allows, in addition to array-like read and write operations, to also use operators such as concatenation, sub-list, length, and more.

Motivation

The idea of having a specialized theory for sequences has been around before. However, it was recently revisited, generalized, and expanded, following a fruitful collaboration between members of the cvc5 team and the move-prover team at Meta (formerly Facebook).

The move-prover is a formal verification tool for smart contracts written in the move language. These are programs that are meant to run on the Diem blockchain, and are written in a resource-aware manner. Given a program and a specification, the move-prover tries to determine whether the program meets the specification. It does so by translating both the program and the specification into an SMT-LIB query, which is unsatisfiable if and only if the program meets its specification. This translation is based on various theories.

Originally, the main theories that were responsible for the encoding of Move’s data structures were the theory of datatypes and the theory of arrays. However, as it turned out, this encoding was not efficient enough, as it involved many quantifiers. A large portion of these quantifiers originated from the need to extend the theory of arrays, which only allows to read and write from an array, with richer operators, such as computing the length, concatenating, and more. This realization led to the idea of introducing a new theory of sequences.

Usage

The documentation for the theory of sequences can be found here. Roughly, it introduces a new sort called Seq, which is parametric. For example, to define the sort of integer sequences, one would write (in SMT-LIB style) (Seq Int). Then, variables that represent sequences can be defined as usual. For example, the following is a declaration of a variable that ranges over sequences of real numbers:

(declare-fun s1 () (Seq Real))

There are various operators that are supported, including the representation of the empty sequence, constructing a sequence from a single element, concatenation of sequences, reading from and updating sequences, reversing the order of the elements, obtaining a sub-sequence, and more.

For example, the following formula (written again in SMT-LIB style) asserts the existence of two non-empty sequences with equal lengths such that the first is the result of reversing the elements in the second, as well as the existence of a third sequence, obtained from the first sequence by changing its first element to be the first element of the second sequence.

This formula is satisfiable, and cvc5 can quickly report satisfiability, and to provide a satisfying model.

(set-logic QF_SLIA)
(declare-fun s1 () (Seq Int))
(declare-fun s2 () (Seq Int))
(declare-fun s3 () (Seq Int))

(assert (= (seq.len s1) (seq.len s2)))
(assert (and (distinct (seq.len s1) 0) (distinct (seq.len s2) 0)))
(assert (= s1 (seq.rev s2)))
(assert (= s3 (seq.update s1 0 (seq.unit (seq.nth s2 0)))))

(check-sat)

Algorithms

cvc5 is able to solve complex formulas that reason about sequences, in combination with a wide variety of other theories that represent the elements of the sequences. How is this done?

The theory of sequences is very similar to the theory of strings. The main differences come from the fact that strings form a very particular instance of sequences, where the domain of the elements is fixed to be the set of Unicode characters. In contrast, the theory of sequences is generic.

Still, the solving techniques for strings can be adapted for sequences. Thus, the core of our implementation is based on an adaptation of the theory-solver for strings. There are two operators, however, that are very common, whose reduction to strings is not very natural: These are seq.nth and seq.update, that read and update elements in sequences. When reducing these operators to existing string operators, the result is a concatenation. For example, asserting that the 5^th element of a sequence x equals to some element e, amounts to asserting the existence of two sequences x1,x2, such that x is the concatenation of x1, the unit sequence [e], and x2.

However, these particular operators are almost identical to the reading and writing operators of the theory of arrays. The only difference is that arrays are completely defined over their entire domain, whereas sequences have a certain length, which introduces the problem of out-of-bounds access (e.g., accessing the 5^th element of a sequence with 2 elements). Thus, existing decision procedures for arrays-based reasoning can also be utilized for solving sequences constraints.

In cvc5, we implemented both approaches. In the first approach, we perform a full reduction of the sequences problem into the (adapted) algorithm for solving strings. In the second approach, we reduce a part of the problem (the part without reading and updating) to strings, while performing array-like reasoning for the reading and writing parts. While the former approach was relatively straightforward to implement and to reason about, the latter introduces many challenges, as combining array-like reasoning with string-like reasoning for the same input formula is far from trivial. More details about this can be found in the 18-pages long correctness proof of our JAR publication regarding this theory. For a more condensed description, check out our IJCAR publication.

Evaluation

To evaluate our implementations, we compared their performance to each other, as well as to the sequences solver of the SMT solver z3. We used two benchmark sets for this evaluation. The first is based on verification conditions that are emitted by the move-prover, and make heavy usage of sequences. The second is a synthetic set of formulas, that are obtained by translating standard benchmarks for the theory of arrays to the theory of sequences. The goal of the first set is to check to what extent our solver can be used in a real-life environment. The second is meant to provide a finer comparison between our two approaches, as they differ only in the operators that are available in the theory of arrays.

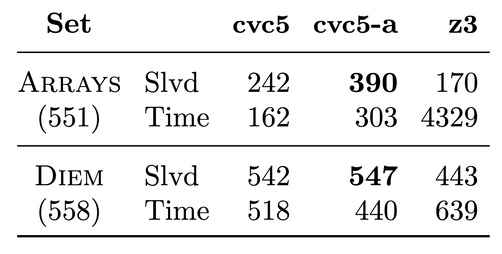
The results are summarized in the following table. In it, cvc5 and cvc5-a refer to the first and second approach, respectively; DIEM and ARRAYS correspond to the first and second benchmark set, respectively. The best configuration overall is the implementation that is based on combining strings and array reasoning.

Overall results.

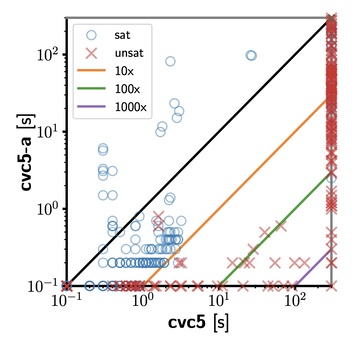
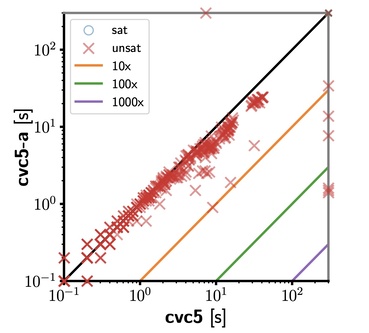
The following two scatter plots compare the two approaches that we implemented, on each benchmark set separately. Other than some exceptions, it is clear that the combination of strings and arrays as a basis for solving sequences constraints performs better.

Arrays-based benchmarks.

move-prover based benchmarks

Conclusion

cvc5 is able to solve constraints about sequences, with a rich set of operators that can be found in standard programming languages (such as concatenation, length computation, reading, updating, and more). The implementation employs two techniques that differ on the way they handle reading from and updating sequences. The solver is capable of efficiently solving both industrial benchmark from the move-prover, as well as hand-crafted ones. Check it out for yourself!

Yoni Zohar is a faculty member at Bar-Ilan University. His research interests are automated reasoning, satisfiability modulo theories, proof theory, and verification.

Check out our GitHub Discussions if you have any questions.

Back to All Blog Posts